The answer to the sleeping beauty problem is 1/2
Too many perpetually-almost-done drafts. I’m entering my ‘just post stuff even if it kinda sucks’ arc.
Note: skip down to the “The halfers are right” section if you’re familiar with the problem and usual positions. Also see the subtitle.
Problem
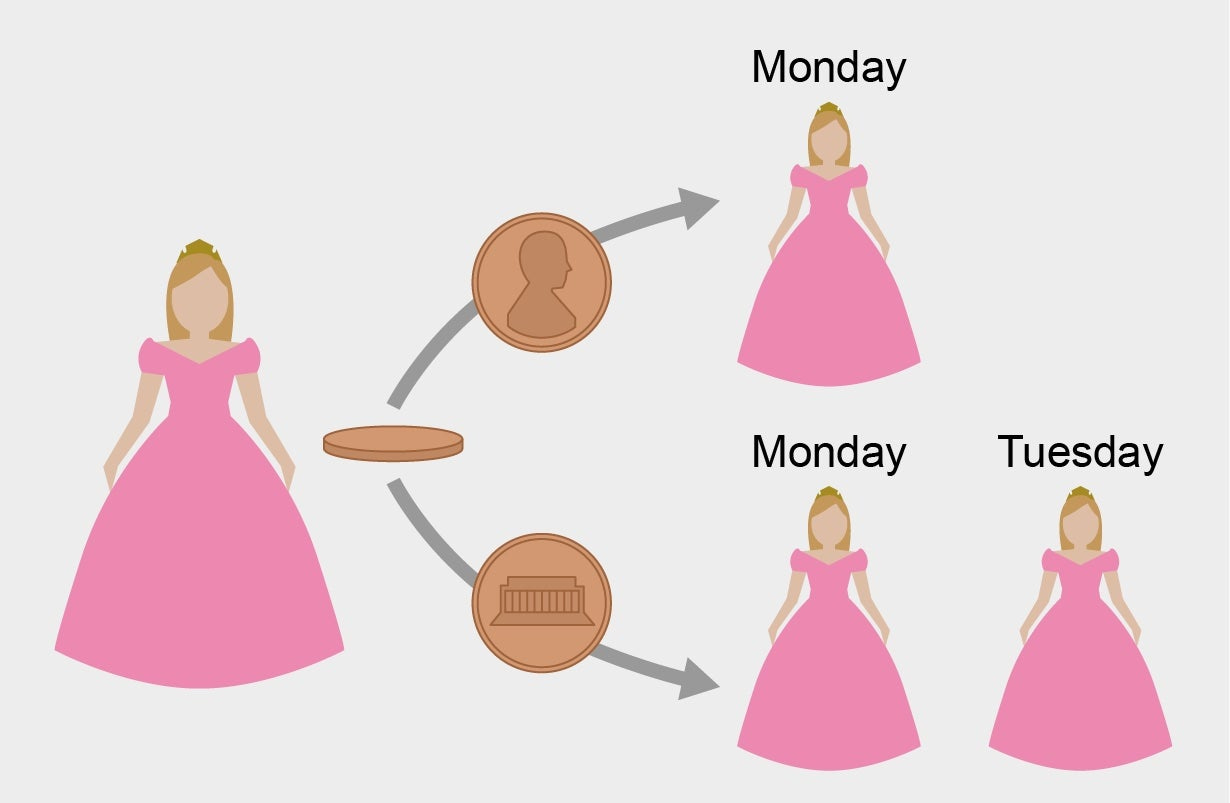
According to Wikipedia, the Sleeping Beauty problem is a “puzzle in decision theory” that goes like this:
Sleeping Beauty [an “ideally rational epistemic agent”] volunteers to undergo the following experiment and is told all of the following details: On Sunday she will be put to sleep. Once or twice, during the experiment, Sleeping Beauty will be awakened, interviewed, and put back to sleep with an amnesia-inducing drug that makes her forget that awakening. A fair coin will be tossed to determine which experimental procedure to undertake:
If the coin comes up heads, Sleeping Beauty will be awakened and interviewed on Monday only.
If the coin comes up tails, she will be awakened and interviewed on Monday and Tuesday.
In either case, she will be awakened on Wednesday without interview and the experiment ends.
Any time Sleeping Beauty is awakened and interviewed she will not be able to tell which day it is or whether she has been awakened before. During the interview Sleeping Beauty is asked: "What is your credence now for the proposition that the coin landed heads?"
(Purported) solutions
There are basically two competing claims about Sleeping Beauty’s subjective probability (recall, as an ‘ideally rational agent’) in the given scenario. Once again, I’ll plagiarize some pseudonymous Wikipedia editors:
Thirder position
The thirder position argues that the probability of heads is 1/3. Adam Elga argued for this position originally as follows:
Suppose Sleeping Beauty is told and she comes to fully believe that the coin landed tails. By even a highly restricted principle of indifference, given that the coin lands tails, her credence that it is Monday should equal her credence that it is Tuesday, since being in one situation would be subjectively indistinguishable from the other. In other words, P(Monday | Tails) = P(Tuesday | Tails), and thus
\(P(\text{Tails and Tues}) = P(\text{Tails and Mon})\)Suppose now that Sleeping Beauty is told upon awakening and comes to fully believe that it is Monday. Guided by the objective chance of heads landing being equal to the chance of tails landing, it should hold that P(Tails | Monday) = P(Heads | Monday), and thus
\(P(\text{Tails and Tues}) = P(\text{Tails and Mon})=P(\text{Heads and Mon}) \)Since these three outcomes are exhaustive and exclusive for one trial (and thus their probabilities must add to 1), the probability of each is then 1/3 by the previous two steps in the argument:
\(P(\text{Tails and Tues}) = P(\text{Tails and Mon})=P(\text{Hears and Mon}) =1/3\)Halfer position
David Lewis responded to Elga's paper with the position that Sleeping Beauty's credence that the coin landed heads should be 1/2…
“Sleeping Beauty receives no new non-self-locating information throughout the experiment because she is told the details of the experiment. Since her credence before the experiment is P(Heads) = 1/2, she ought to continue to have a credence of P(Heads) = 1/2 since she gains no new relevant evidence when she wakes up during the experiment. This directly contradicts one of the thirder's premises, since it means P(Tails | Monday) = 1/3 and P(Heads | Monday) = 2/3.
Maybe we should care?
Apparently this might somehow matter for philosophical anthropics, which in turn might somehow matter for the fate of the humanity.
Again, Wikipedia: “credence about what precedes awakenings is a core question in connection with the anthropic principle.”
The halfers are right
Argument:
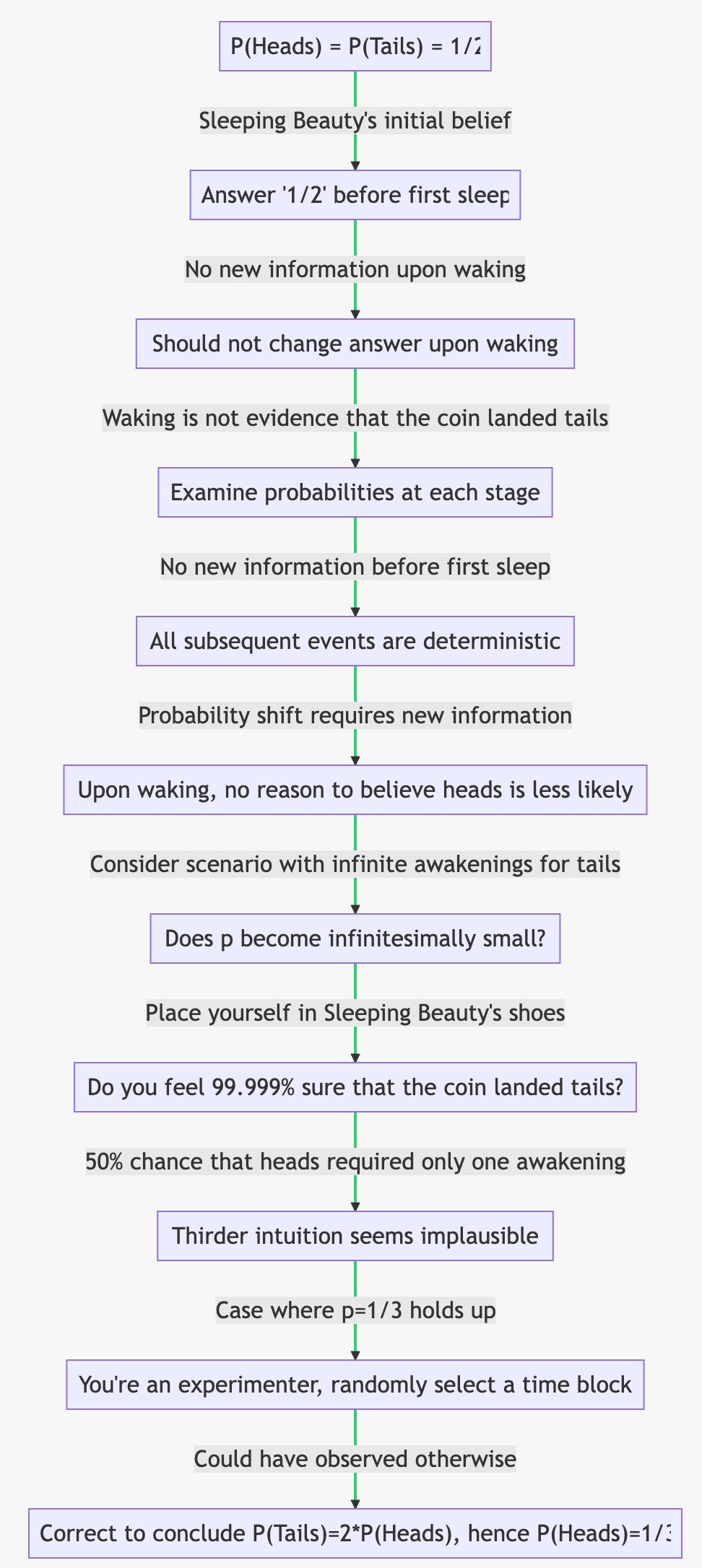
By assumption, P(Heads) = P(Tails) = 1/2, so Sleeping Beauty would answer “1/2” before being put to sleep for the first time.
Sleeping Beauty gains no new information upon waking.
Therefore, she should not change her answer upon waking.
Point 21 is where the dispute lies and so is worth defending more fully.
Claim: waking is not evidence that the coin landed tails
Let us examine the probabilities at each stage of events in this setup. Initially, the coin's probability p is 1/2 before it is flipped. At this point, Sleeping Beauty would also say p equals one-half. For this to change, some new information must be introduced.
Before she goes to sleep for the first time, has anything occurred between when the coin landed (out of her sight) and her falling asleep? The answer is no; everything remains symmetrical with a probability of one-half. Since all subsequent events are deterministic, Sleeping Beauty can devise an algorithmic plan based on what happens next.
However, for the probability to shift from one-half to any other value like one-third or even zero (as thirders claim), Sleeping Beauty would have to acknowledge that upon waking up – despite knowing she cannot differentiate between worlds – she will instantly believe that heads now have a lower likelihood than previously thought.
An intuition pump
To further illustrate where thirders err in their reasoning, consider an alternative scenario: instead of being woken up twice if tails, imagine it happening a billion times or even countably infinite times. In such cases, p should equal zero or an infinitesimally small number according to the same reasoning that implies p=1/3.
Now place yourself in Sleeping Beauty's shoes as you awaken; do you really feel 99.999% sure that the coin landed tails? I certainly don’t, in a sense that seems intuitively much clearer than introspecting on the 1/2 vs 1/3 case.
Indeed, it seems implausible given there remains a 50% chance that heads appeared and only required waking on just one occasion - which, of course, might have occurred just a moment ago.
So where does the thirder intuition come from?
It’s hard to say, but I think a case in which p=1/3 really does hold up gestures towards the answer:
Suppose you’re one of the experimenters, and divide the days of Monday and Tuesday into half-hour chunks. You then randomly select one, and find out that during this block Sleeping Beauty happened to be woken by your colleague.
Since this time you could have observed otherwise (unlike Sleeping Beauty in the thought experiment discussed), you’d be correct to conclude that that P(Tails)=2*P(Heads), which implies in this case P(Heads)=1/3.
Really, this subtitle is just a more forthright reformulation of “Sleeping Beauty gains no new information upon waking.”


If you wake up and I offer you a bet on what day it is, what odds do you accept?
The correct answer is 1/3.
"Waking is not evidence that the coin landed tails." Nobody say it is. It is an opportunity to observe a consequence of the outcomne of a 50:50 random experiment, not an event. The error made by halfers, is confusing the result of the experiment with this opportunity. Since the possibility of this observation depends on the result, it is evidence.
There are two possible observations THAT ARE MADE INDEPENDENT by the amnesia drug. The evidence is that the ability to make an observation is denied in some situations when the result is HEADS, but it can always be made if it is TAILS. So the conditional probabilities of those two results, given that an observation is being made, cannot be the same. "HEADS" has to be diminished relative to "TAILS." This argument does not prove that 1/3 is correct, but it does prove that 1/2 cannot be.
And the real issue is that the setup you cite does not match the actual problem. You can look it up in Adam Elga's paper. It is the way he tried to solve the original problem. The original problem does not mention Monday, or Tuesday, or define a difference between the possibility an observation on those two days. It just says that you (it was phrased on the first person) will be woken once if HEADS and twice if TAILS. Elga first created the scheduling difference, and then eliminated it by "telling" the subject two different pieces of information. As you detailed. There is a better way, that makes each possible observation the same and allows a trivial solution.
On Sunday Night, after SB is asleep, flip two coins. Call them C1 and C2.
On Monday, if both coins are showing HEADS, let SB sleep thru the day. But if either is showing TAILS, wake her, and ask her "What is your credence now for the proposition that coin C1 is showing HEADS?" After she answers, put her back to sleep with amnesia.
On Monday Night, when SB is again (or still) asleep, turn coin C2 over.
On Tuesday Morning, if both coins are showing HEADS, let SB sleep thru the day. But if either is showing TAILS, wake her, and ask her "What is your credence now for the proposition that coin C1 is showing HEADS?" After she answers, put her back to sleep with amnesia.
There are still the two observation opportunities that the original problem asked for. But now they are, as far as probability is concerned, identical. So we can solve that one-day problem, not the two-day one. When the two coins were examined this morning, there were four equally-likely combinations: HH, HT, TH, and TT. But since SB was awakened, she knows that HH is eliminated. The remaining three, HT, TH, and TT are still equally likely, and in only one is coin C1 showing HEADS.
The answer is proven to be 1/3.