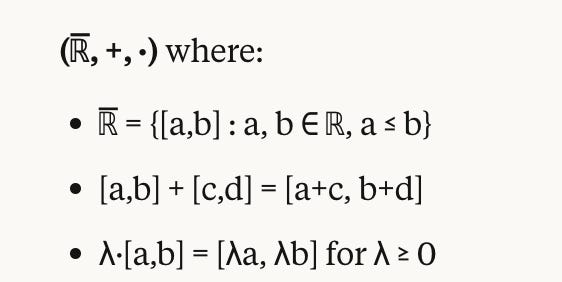A while back I wrote the post “Suffering-focused total utilitarianism: Total utilitarianism doesn't imply that suffering can be offset” and I basically stand by it.
The post isn’t that long, but here’s an LLM summary which I admit adds a bit of structural clarity even before I introduce some additional substantive points of clarification below:
Summary of the original post
Core Claim: Even within a utilitarian framework that treats happiness and suffering as commensurable values on a single moral axis, some instances of suffering may be morally incommensurable with any finite or infinite amount of happiness.
The Argument
P1. A perfectly rational, self-interested hedonist would refuse certain trades (e.g., one week of maximal torture for any amount of happiness, however large or long-lasting).
P2. The preferences of this idealized agent reveal either (a) our own idealized preferences or (b) what is morally valuable, all else equal.
P3. There exists no compelling argument that all suffering can in principle be offset by sufficient happiness.
P4. In the absence of such arguments, we should defer to the intuition that some suffering cannot be morally offset.
C. Therefore, some instances of suffering cannot be ethically outweighed by any amount of happiness.
The Mathematical Challenge
Standard utilitarianism implicitly assumes hedonic states map to the real numbers, enabling cardinal comparisons and trade-offs. However:
Ordinal ≠ Cardinal: While hedonic states must be ordinally comparable (we can rank them), this doesn't entail they possess cardinal magnitudes that behave like simple real numbers
Alternative Models: The relationship between suffering and offsetting happiness might be better modeled by a function with a vertical asymptote—where beyond some threshold of suffering, no amount of happiness can provide equivalent value.
Against the Standard Defense
Karnofsky's argument (that we accept small risks of terrible outcomes for modest benefits, therefore any harm can be offset) fails because:
It conflates removing goods (death) with instantiating suffering (torture)
It extrapolates from weak evidence (our flawed risk-taking behavior) to strong metaphysical claims
It assumes without argument that probability calculus applies uniformly across all magnitudes of suffering
Implications
This view preserves total utilitarianism's core structure while rejecting the assumption that all values are mathematically tractable. Some suffering may constitute a moral catastrophe that no amount of flourishing can justify—not because suffering and happiness are incomparable, but because their relationship is asymptotic rather than linear.
1) My sin: some conflated claims
In the original post, I didn’t distinguish clearly enough between a couple highly related but distinct claims. It actually gets more granular than this, but here are the two big ones:1
The weaker logical/mathematical claim that offsetability isn't implied by standard utilitarianism.
Or really, to be pedantic but a bit more specific: that offsetability isn’t implied by the set of claims/premises that seem to be the consensus conceptual basis and content *of* utilitarianism. More on this below.
The stronger metaphysical claim that some suffering actually cannot be offset.
The issue is one of argumentative and rhetorical clarity. As the subtitle of this post suggests, I don’t think this failure undermines the validity and likelihood of the underlying claims themselves.
2) Clarifying [total] “utilitarianism”
To the best of my knowledge, there are five consensus premises that are necessary and sufficient to imply and constitute [total] utilitarianism2
Consequentialism: The rightness of actions depends solely on their consequences (the states of affairs they bring about), not on the nature of the acts themselves or adherence to rules.
Welfarism: The only thing that matters morally in evaluating consequences is the wellbeing (welfare/utility) of sentient beings. Nothing else has intrinsic moral value.
Impartiality/Equal Consideration: Each being's wellbeing counts equally - a unit of wellbeing matters the same regardless of whose it is. No special weight for yourself, your family, your species, etc.
Aggregation/Sum-ranking: The overall value of a state of affairs is determined by summing individual wellbeing. More total wellbeing is better.
Maximization: We ought to bring about the state of affairs with the highest total value (maximum aggregate wellbeing).
To be clear, these five things are just what I mean by “[total] utilitarianism”.
I don’t think this bit is very contentious, but of course please pushback if you think this is wrong.
Anyway, I think my argument for the logical claim (point 1 above) becomes significantly clearer when you make all this explicit:
My claim
Claim: the above five premises do not imply offsetability. Full offsetability requires an additional sixth premise that describes what kinds of mathematical model accurately and adequately model the real world.
The most intuitive and common such premise I believe to be the following:3
Real-number representation: All states of hedonic welfare are adequately modeled by the real numbers (with standard arithmetic operations).
Without such an additional premise, the standard utilitarian framework doesn't entail that any amount of suffering can be offset by sufficient happiness.
It’s perfectly coherent to argue that premise 6 is in fact true. Maybe it is. To quote myself from the original:
Perhaps hedonic states really are cardinally representable, with each state of the world being placed somewhere on the number line of units of moral value; I wouldn’t be shocked. But if God descends tomorrow to reveal that it is, we would all be learning something new.
A note on math
I’ll clarify that I am not objecting to any sort of pure mathematical claim. Rather, I’m beefing with the usually-implicit substantive metaphysical claim that relates pure mathematics to the real world.
On the Von Neumann-Morgenstern utility (VNM) theorem
The only counterarguments I’ve heard to my logical claim involve the Von Neumann-Morgenstern utility theorem. I do not find these very convincing.
Check out Wikipedia (linked above) for the formal definition, but here’s Claude’s summary in plain-ish English:
The Setup
Consider an agent choosing between lotteries - probability distributions over outcomes. A lottery L might be: "30% chance of outcome A, 70% chance of outcome B."
The agent has preferences (≻) over these lotteries: L ≻ M means "the agent prefers lottery L to lottery M."
The Four Axioms
Completeness: For any two lotteries, the agent either prefers one or is indifferent.
Philosophically: The agent has determinate preferences over all options.
Transitivity: If L ≻ M and M ≻ N, then L ≻ N.
Philosophically: Preferences are coherent/non-cyclical.
Continuity: If L ≻ M ≻ N, there's some probability p where the agent is indifferent between M and "lottery p·L + (1-p)·N."4
Philosophically: No outcome is lexically superior - everything has a "price" in probability terms.
Independence: L ≻ M if and only if [p·L + (1-p)·N] ≻ [p·M + (1-p)·N] for any N and p∈(0,1).
Philosophically: Irrelevant alternatives don't affect relative preferences. If you prefer coffee to tea, you still prefer "coffee or death (50-50)" to "tea or death (50-50)."
The Theorem
If an agent's preferences satisfy these four axioms, then there exists a utility function u such that:
The agent prefers lottery L to lottery M if and only if E[u(L)] > E[u(M)]
This function is unique up to positive affine transformation (multiplying by a positive constant and adding any constant)
Response
VNM does imply that agents whose preferences satisfy those four criteria above can be turned into a real-valued (i.e., modeled adequately by the set of real numbers) utility function, but it’s totally logically possible, coherent, and plausible to reject continuity (premise 3). Indeed, that’s exactly what lexical, non-offsetable preferences are doing:
And importantly: not only is it logically possible, but nothing particularly weird or implausible happens if you reject this premise. Again, to quote an LLM:
No money pump problems: If I lexically prefer "not being tortured" over "any amount of money," you can't construct a sequence of trades that leaves me strictly worse off. My preferences remain transitive and complete - I just refuse certain trades categorically.
…
What you keep:
Immunity to Dutch books
Transitivity and completeness
Perfectly coherent decision-making
In simpler terms, rejecting continuity doesn’t imply any sort of epistemic red flag. No money pumps, no loss of coherence, no cognitive dissonance necessary; the world keeps turning.
Conclusion
Standard total utilitarianism, defined by consequentialism, welfarism, impartiality, aggregation, and maximization, does not imply that any instance of suffering can be “offset” or morally justified by sufficient happiness.
That requires an additional sixth premise: that welfare states map cleanly onto the real numbers with standard arithmetic operations. This is a substantive metaphysical claim about the nature of suffering and happiness that usually gets smuggled in without justification.
Recognizing that offsetability isn't mathematically required by utilitarianism itself opens up conceptual space for suffering-focused views that preserve the structure of and very compelling (and I think true) arguments for total utilitarianism in some form.
If you find this argument important and compelling and like doing this kind of thing, I’d be interested in turning it into a proper arXiv PDF - feel free to reach out to aaronb50[at]gmail.com! Bonus points for having more philosophy training/experience than me!
Thanks to Claude Opus 4.1 for much help with this article and Rob Long for discussion that led to it.
There’s a sort of intermediate claim between (1) and (2) that’s essentially “plausibility: not only is non-offsetability logically permitted by utilitarianism, but it is basically plausible given what we know about ethics and what the world is like”
I am using the terms “utilitarianism” and “total utilitarianism” to mean the same thing.
Update a few hours after publication:
I edited this section response to a good critique by Max Alexander, which is that there are other mathematical systems besides the standard real numbers + arithmetic one that would then also entail offsetability.
I’m not smart enough to have a formal proof + formal criteria for what kinds of math/model/ontology do preserve offsetability but I think the (somewhat contrived) of example of closed real-valued intervals with interval addition and scalar multuplication works. That is:
Note that p cannot be 0 or 1 here, as this would imply indifference between some of the options but we are taking as a hypothesis that the preference ordering is strict.